Matematika Blogger

Gerak parabola
Asumsi pertama tidak ada gaya dengan arah horizontal
F_x=0
Hukum Newton maka
F_x=mx ̈
Karena F_x=0 maka

x ̈=0
x ̇=∫▒〖0 dt=C〗 ;C= B_1
x ̇=B_1
x(t)=∫▒〖B_1 dt〗
=B_1 t+B_2
Jika
x(0)=x_0 maka
x(0)=B_1.0+B_2=B_2
x_0=B_2
x ̇(0)=V_(x0 ) B_1=V_xo
=B_1 B_2= x_0
Jika tidak mengalami gesekan udara maka
{█(x ̈=0@( y) ̈=-g)┤


{█(x(t)=B_1 t+B_2@y(t)=-1/2 〖gt〗^2+D_1+D_1 )┤

unit Unit1;

interface

uses
Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms,Dialogs, StdCtrls, ExtCtrls, DBCtrls, Grids, DBGrids, DB, DBTables, jpeg;

type
TForm1 = class(TForm)
Table1: TTable;
DataSource1: TDataSource;
DBGrid1: TDBGrid;
DBNavigator1: TDBNavigator;
Label1: TLabel;
Label2: TLabel;
Label3: TLabel;
Edit1: TEdit;
Edit2: TEdit;
bkeluar: TButton;
Image1: TImage;
procedure bkeluarClick(Sender: TObject);
procedure Edit1Change(Sender: TObject);
procedure Edit2Change(Sender: TObject);
private
{ Private declarations }
public
{ Public declarations }
end;

INSERT
INSERT INTO mahasiswa VALUES ('F1A108007','RAHMAT','L','KAMPUS')
INSERT INTO <nama tabel> VALUES (nama kolom>
INSERT INTO mahasiswa (nim,namamhs,jk) VALUES ('F1A108007','RAHMAT','L')

UPDATE
UPDATE mahasiswa SET namamhs='SAFAR' WHERE nim='F1A108007'

DELETE
DELETE FROM mahasiswa WHERE nim='F1A108007'
DELETE FROM mahasiswa WHERE NAMAMHS='RAHMAT'

MENAMPILKAN DATA

SELECT <nama kolom> FROM <nama tabel>

SELECT * FROM mahasiswa
SELECT nim,namamhs FROM mahasiswa


SELECT NIM, Nama_Mahasiswa, Nama_MK, SKS, Sem_ke, Tahun_Akademik, Semester, Nilai FROM kuliah, nim, kodemk WHERE kuliah.NIM = nim.NIM AND kuliah.Kode_MK = kodemk.Kode_MK

SELECT NIM, Nama_Mahasiswa, Kode_MK, Nama_MK, Tahun_Akademik, Semester, Nilai FROM kuliah, kodemk, nim WHERE kuliah.Kode_MK = kodemk.Kode_MK AND nim.NIM = kuliah.NIM AND (kuliah.NIM='F1A108007' OR kuliah.NIM='F1A107038')


UNTUK MENAMPILKAN STAMBUK MATEMATIKA SAJA
SELECT * FROM MAHASISWA WHERE NIM LIKE'F1A1%'
SELECT * FROM MAHASISWA WHERE NIM LIKE'F1A1_____'(TANDA (_) SEBANYAK 5 KALI)

UNTUK MENAMPILKAN SEMESTER MATAKULIAH
SELECT * FROM MATAKULIAH WHERE semke= 1 or semke= 3 or semke= 5

UNTUK MENGURUTKAN DATA MISAL BERDASARKAN NAMA MAHASISWA
SELECT * FROM MAHASISWA WHERE NIM LIKE'F1A1%' ORDER BY NAMAMHS ASC/DESC

UNTUK MENGHITUNG JUMLAH BARIS
SELECT COUNT (*) FROM MAHASISWA

UNTUK MENGHITUNG TOTAL NILAI
SELECT SUM (Nilai) FROM kuliah


UNTUK MENAMPILKAN NAMA DIANTARA NIM
SELECT * FROM MAHASISWA WHERE NIM BETWEEN 'F1A101004' AND 'F1A102001'



MENCARI DENGAN QUERY DENGAN NAMA
procedure TForm1.Button1Click(Sender: TObject);
begin
  query1.SQL.clear;
  query1.sql.Add('select NIM, Nama_Mahasiswa, Kode_MK, Nama_MK, Tahun_Akademik, Semester, Nilai');
  query1.SQL.Add('FROM kuliah k, kodemk km, nim mh');
  query1.sql.Add('WHERE k.NIM=mh.NIM AND km.Kode_MK=k.Kode_MK');
  query1.SQL.Add('AND Nama_Mahasiswa LIKE :NM');
  query1.Prepare;
  query1.ParamByName('NM').AsString :='%'+edit1.text+'%';
  query1.Open;
end;

end.

MENCARI DENGAN QUERY DENGAN STAMBUK DAN NAMA
procedure TForm1.Button1Click(Sender: TObject);
begin
  query1.SQL.clear;
  query1.sql.Add('select NIM, Nama_Mahasiswa, Kode_MK, Nama_MK, Tahun_Akademik, Semester, Nilai');
  query1.SQL.Add('FROM kuliah k, kodemk km, nim mh');
  query1.sql.Add('WHERE k.NIM=mh.NIM AND km.Kode_MK=k.Kode_MK');
  query1.SQL.Add('AND (Nama_Mahasiswa LIKE :NM OR NIM LIKE NM)');
  query1.Prepare;
  query1.ParamByName('NM').AsString :='%'+edit1.text+'%';
  query1.Open;
end;

end.

 RUANG DUAL

μ : { (v,w) ∈ μ | μ (w) = v  1 }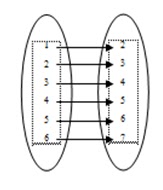     
1. Injekif
Misal w₁                                    μ(w₁) = Lw₁
2. Surjektif

.

+

Berdasarkan definisi, misal V = {V, F ; + , . , , }

+

Adalah ruang vektor atas lapangan F. Suatu pemetaan h: V → W disebut homomorfisma, jika untuk semua v₁ , v₂ ∈ V dan semua α ∈ F,