RUANG DUAL
16.06 | Author: rahmat
 RUANG DUAL

Teorema 3.4 :
Misal V ruang Hermit yang berdimensi hingga maka pemetaan μ : w ∈ V Lw ∈ V* adalah bijektif.
Jadi μ : w ∈ V Lw ∈ V* korespondensi 1-1 dari V ke V*.
Bukti:
Akan dibuktikan bahwa μ : w ∈ V Lw ∈ V* merupakan pemetaan bijektif yaitu dengan menunjukkan bahwa pemetaan tersebut merupakan pemetaan injektif dan surjektif. Contoh pemetaan injektif dan surjektif (bijektif) yaitu sebagai berikut :
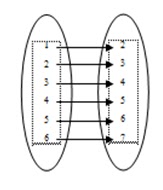
μ : v w
v = {1,2,3,4,5,6}
w = {2,3,4,5,6,7




μ : { (v,w) ∈ μ | μ (w) = v  1 }     

1. Injekif

Misal w1                                    μ(w1) = Lw1
               w2                                     μ(w2) = Lw2
       jika μ(w1) = μ(w2) maka w1 = w2
                      Lw1 (v) = Lw2 (v)
                     <v,w1> = <v,w2>
                     <v,w1> - <v,w2> = 0
                    <v,w1 - w2> = 0, untuk setiap v ∈ V.
Karena V definit positif, maka w1 – w2 = 0, berarti w1 = w2. Jadi jika μ(w1) = μ(w2), maka w1 = w2, sehingga μ = injektif     

2. Surjektif

w1* = Lw1 = < - ,w1>
w2* = Lw2 = < - ,w2>

Akan ditunjukkan bahwa Im (μ) itu ruang bagian dari V*.
Ambil dua elemen sebarang dalam Im (μ) misal w1* dan w2*, maka
w1* =  < - ,w1>
w2* = < - ,w2>
w1* - w2* = < - ,w1> - < - ,w2>
                = < - , w1 - w2 >
                = Lw1 – w2 ∈ Im (μ).
Sebab w1 – w2 ∈ V dan μ = injektif. Sehingga w1­­­­* - w2­* ∈ Im (μ) subgroup dari V* terhadap addisi (penjumlahan).
Ambil c ∈ C, w* ∈ Im (μ), maka w* =Lw.
                 cw* = c.Lw
                                    = c.< - ,w>
                        = < - , w>
                       =  ∈ Im (μ) sehingga cw* ∈ Im (μ).
Jadi Im (μ) ruang bagian dari V*.
Akan dibuktikan bahwa dim [ Im (μ)] = dim (V).
Misal {x1, x2, x3, ... , xn} basis dari V, akan ditunjukkan bahwa (μ(x1), μ(x2), μ(x3), ... , μ(x1n)} basis dari  Im (μ).
Ambil sebarang y ∈ Im (μ), maka y = μ(x) untuk suatu x ∈ V.
                 x =   1x1 + 2x2 + ... + nxn
           μ(x) = μ( 1x1 + 2x2 + ... + nxn )
                   = L 1x1 + 2x2 + ... + nxn
                         = < - , 1x1 + ... + nxn>
                   = < - , 1x1> +...+ < - , nxn>
                   = 1 .< - , x1> +...+ n .< - , xn>
                   = 1Lx1 +...+ nLxn
                   = 1 μ(x1) +...+ n μ(xn)
Jadi y = μ(x) = 1 μ(x1) +...+ n μ(xn)
Ambil kombinasi linier sebarang,
                 β1 μ(x1) + β2 μ(x2) +...+ βn μ(xn)          = 0
                 μ( 1x1) + μ( 2x2) +...+ μ( nxn)             = 0
                 μ( 1x1+ 2x2 +...+ nxn)                       = 0
.

+
Berdasarkan definisi, misal V = {V, F ; + , . , , }
                                            W = { W, F ; + , . ,    , ,    }}
+
Adalah ruang vektor atas lapangan F. Suatu pemetaan h: V → W disebut homomorfisma, jika untuk semua v1 , v2 ∈ V dan semua α ∈ F,
h (v1 v2)= h (v1)         h (v2)
dan
h (α v1)= α h (v2)
jika setiap vektor dari W berada dalam Im(h), h disebut homomorfisma dari V pada W.
(jadi μ = homomorfisma group terhadap addisi)
Karena μ = homorfisma group yang injektif, maka
1x1 + 2x2 +...+ nxn               = 0
Maka        1 = 2 = ... = n                       = 0
Jadi           β1 = β2 = ... = βn                       = 0
Jadi           {μ (x1), μ (x2), ... , μ (xn)} adalah basis dari Im (μ).
Karena banyaknya n, maka dim (V) = dim [Im (μ)] = n,
padahal dim (V) = dim (V*), akibatnya dim [Im (μ)] = dim (V*).
Karena Im (μ) ruang bagian dari V* dan mempunyai dimensi yang sama dengan V*, maka Im (μ) = V*
Karena Im (μ) = V* dan μ = injektif, maka μ = surjektif. Jadi μ = bijektif.
|
This entry was posted on 16.06 and is filed under . You can follow any responses to this entry through the RSS 2.0 feed. You can leave a response, or trackback from your own site.

0 komentar:

Posting Komentar